Lean 函数式编程(一) | 了解 Lean
唠唠闲话
关于 Lean 的函数式编程第一章,编程基础,了解 Lean 的基本概念,包括数据结构,多态,以及语法特性。
基础概念
交互方式
Python, Java, C# 这类语言通常提供一个 REPL(Read Eval Print Loop)用于交互式地执行命令;而 LEAN 语言服务器协议(LSP)的扩展版本,将交互功能集成到编辑器上(比如 vscode),用户在输入命令的同时,在编译器上获取反馈。
如果我们希望计算某个表达式的值,使用 #eval 命令:
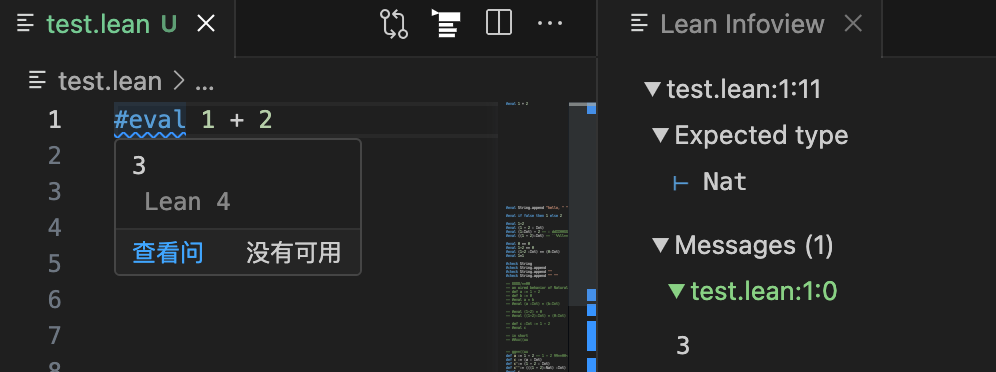
1 | #eval 1 + 2 |
通过查看右侧面板,或者将鼠标光标放在 #eval 上,查看表达式取值。
为方便展示,我们用注释的形式将显示结果写在代码下方,LEAN 的注释格式有两种:单行注释 -- 和多行注释 /- ... -/。
边际效应
大多数语言都是命令式的(imperative),程序由一系列执行语句组成,用于计算结果。此外,程序能访问到变量的内存,并在执行过程中修改变量的取值。因为这种可修改的特性,这些程序通常存在边际效应(side effects),比如某个表达式的值可能会因为执行顺序的不同而不同。
关于边际效应,用几个例子讲讲我的理解。在下边的 Python 代码中,函数 f 依赖于变量 a,而变量 a 的修改会导致 f 执行结果变化:
1 | a = 1 |
类似地,在 C 数组中,如果我们修改了数组 a 的值,那么指向 a 的指针 b 的值也会发生变化:
1 | int a[2] = {1, 2}; |
但在 LEAN 中,程序都是表达式,其取值是确定不变的。Haskell 和 LEAN 都具有这个特性,而且在 .hs 或 .lean 文件如果对一个变量做多次定义编译器会抛出错误。由于 Haskell 还支持交互式编程,我们用 Haskell 来解释这个特性:
1 | ghci> a = 1 |
在最开始定义 f 的时候,不是将 a 放入函数体,而是放入 a 的值。所以修改 a 并不会影响 f,而且 f 每次执行的结果都是确定不变的。此外,像 a=1;a=2 这种变量重定义仅在 REPL 中有效,在 .hs 文件中仍然会报错。
类似地,LEAN 的判断语句也是一个表达式,而且 if 必须伴随 else,因为表达式取值必须是确定的,不存在 Null 取值。
1 | #eval if 1 > 2 then 1 else 2 |
本节回顾:无边际效应,所有程序都是表达式,不允许对一个变量做多次定义或修改。
变量、函数和类型
类型在程序中有很多作用,比如
- 允许编译器决定变量在内存中的存储方式
- 帮助程序员向其他人传达意图,限定程序输入输出的规范
- 防止各种潜在错误,不匹配类型的数据运算
- 帮助 LEAN 编译器生成辅助代码
LEAN 的所有程序本质都是表达式,且表达式都有其类型。通常,编译器会进行自动推断来判读表达式类型,但也可以声明类型
1 | #eval (1 + 2 : Nat) -- 自然数类型 Nat |
我们可以通过 #check 来检查类型。
1 | #check 1 + 2 |
在函数式编程语言中,函数是一等公民。这个特性在 Haskell 和 LEAN 语言上更加明显,它们甚至连定义格式也是完全一致的,变量就是函数的特殊情形。
LEAN 通过 def 关键字定义变量,其中赋值号用 := 而不是 =,后者被用于判断语句。
1 | def x := 1 -- 定义 Nat 类型的变量 x |
变量的定义格式为 def 变量名 : 类型 := 表达式,其中 类型 可以省略,编译器会自动推断。至于函数的定义格式,在 := 左边添加参数就得到了:
1 | def f (x : Nat) := x + 1 -- 一参函数 |
函数的定义格式为 def 函数名 (x1 x2 ... : 类型) (y1 y2 ...: 类型) ... : 返回类型 := 表达式,由于编译器会自动推断,变量的类型也可以省略。
从这里不难看出,变量本质上就是零参数的函数。
此外 LEAN 的函数调用不需要加括号,f x y 等同于 f(x, y),比如
1 | #eval String.append "hello, " "lean!" |
同样地,我们可以用 #check 来检查函数类型,但需加上括号,否则返回的是函数签名(signature)。
1 | #check f -- 返回函数签名 |
多参函数的类型是 Int → Int → Int,根据映射的右结合律,可以理解为 Int → (Int → Int)。也即,二参函数 myplus 由两个单参函数复合而来,其中第一个函数返回值是个单参函数。具体地,我们可以只传递一个参数,并查看返回结果
1 | def addone := myplus 1 |
这种多参转化为单参的方式称为柯里化(curring),以数学家 Haskell Curry 命名。
和通常的语言相比,LEAN 有一个最不寻常的特性,它的类型也是一等公民。举个例子,假设你觉得 String 这个名字太长,那可以定义一个新的类型 Str 来代替它
1 | def Str : Type := String -- 将 String 作为传入参数!!! |
新类型 Str 赋值为 String,能沿用针对 String 的运算,比如
1 | def connectString (str1 str2 : String) := str1 ++ str2 |
尽管 connectString 传入参数要求 String 类型,但使用 Str 也是符合的。至于输出结果为 String 而不是 Str,这是 connectString 输出类型决定的。
新手在这里可能遇到一个错误:现在假设我们觉得用 Nat 表达自然数太简短,想用 NaturalNumber 来代替,那么定义
1 | def NaturalNumber : Type := Nat |
接着定义变量 a,这将产生错误
1 | def a : NaturalNumber := 1 |
这个错误源于 LEAN 的一个特殊机制:数字输入的重载特性。为了适应不同的类型需求,当我们在使用数字 1,2,3... 时,如果编译器能判断数字取什么类型有意义,这些数字 123... 才开始匹配转化为类型。
1 | def a := 1 |
输入 1 得到 Nat,输入 -1 得到 Int,通过指定类型 1 也可以得到 Int。
而当执行 1 : NaturalNumber 时,编译器并不知道 1 应该适应为什么类型,正确写法应当是
1 | #eval ((1 : Nat) : NaturalNumber) |
通过添加括号来让 1 有意义,继而在转化为 NaturalNumber。或者我们再举一个例子,
1 | #eval 1-2 -- 1 和 2 默认为 Nat,运算得 0 |
顺带一提,冒号 : 的优先级极低,经常要结合括号使用。
这个机制很奇怪。
Haskell 的处理方式很自然,通过参数化的Num a => a来表示数字类型,以此支持不同类型数值的运算。
LEAN 重载的规则里,1本身没有类型,如果简单地理解为Nat类型,在运算(1-2):Int中会先得到0:Nat,然后转化为Int,这样就不对了。
可能整体学下来会有新的理解,附一段原话:
This error occurs because Lean allows number literals to be overloaded. When it makes sense to do so, natural number literals can be used for new types, just as if those types were built in to the system. This is part of Lean’s mission of making it convenient to represent mathematics, and different branches of mathematics use number notation for very different purposes. The specific feature that allows this overloading does not replace all defined names with their definitions before looking for overloading, which is what leads to the error message above.
后记:Lean 的数字是允许重载地,也即,可以像定义加减法一样,把数字当符号来重载。处理数字 n 时,先得到自然数,然后根据重载规则,把 n 转化为对应的类型。
在一些场景中,比如希望用简写 N 代替 Nat,可以用 abbrev 关键字,类似 C 语言的 #define。
1 | abbrev N : Type := Nat |
在幕后,一些定义会在重载解析期间被内部标记为可展开的,而另一些则不会标记。可展开的定义称为可约的(Reducible)。控制可约性对 Lean 的灵活性而言至关重要:完全展开所有的定义可能会产生非常大的类型,这对于机器处理和用户理解来说都很困难。使用 abbrev 生成的定义会被标记为可约定义。
本节回顾:
- Lean 的所有程序本质上都是表达式,都存在类型,可以通过
#check来检查。 - 在函数式编程语言中,函数是一等公民。实际上,变量等同于零参数的函数。
- 一般地,函数定义格式为
def 函数名 (x1 x2 ... : 类型) (y1 y2 ...: 类型) ... : 返回类型 := 表达式,包括四个部分,函数名,输入参数类型,输出类型,表达式。由于编译器会自动推断,变量类型也可以省略。 - Lean 函数经常省略括号,比如
f x y理解为f(x, y)或者从柯里化的角度理解为(f x)(y),即通过两个单参数函数复合得。从类型上看,Lean 满足右结合率,比如Int → Int → Int理解为Int → (Int → Int)。 - Lean 不仅函数是一等公民,甚至类型也是一等公民。
abbrev关键字可以为一些变量设置缩写,比如简写类型名称。
结构体
结构体常用于为表达复杂数据,LEAN 的结构体使用 structure 关键字定义:
1 | structure Point where |
最后一行 deriving Repr 生成默认显示,方便 #eval 打印结果的输出,作用类似于 Python 的 __repl__ 方法。如果该行缺省在执行 #eval 时会报错。
结构体通过 {} 来构建,比如
1 | def origin : Point := { x := 0, y := 0 } |
定义两点的加法函数
1 | def addPoints (p1 : Point) (p2 : Point) : Point := |
最后一个例子报错,因为 LEAN 无法推断 {} 的数据类型,而第一处 #eval 不会报错,因为 LEAN 从 addPoints 函数推断了数据为 Point。
由于 LEAN 的变量不可变,如果要修改变量的某个字段,比如把点 {x:=1, y:=2} 的 x 取值为 0,只能创建新变量:
1 | def zeroX (p:Point) : Point := { x := 0, y:= p.y } |
但如果结构体的字段非常多,可以用 with 语法修改特定字段,把其他照抄:
1 | def zeroX (p:Point) : Point := { p with x := 0 } |
前边例子用 origin.x 获取字段 x 的值,这本质上是执行了一个函数 Point.x
1 | #check Point.x -- 查看函数签名 |
这是 LEAN 针对 . 的一个语法,p.func 会执行 Point.func 函数,并以 p 作为匹配到的最左侧的参数。
举个例子,定义结构体上的函数 Point.modifyBoth:
1 | def Point.modifyBoth (f : Float → Float) (p : Point) : Point := |
这里定义了 Point.modifyBoth 函数,其接受两个参数,且第二参为最左侧的 Point 类型参数。执行 p.modifyBoth f 等同于调用 Point.modifyBoth f p。
除了定义 Point 时的字段 x, y,结构体默认还定义了构造子 Point.mk,用于构造 Point 类型的数据。比如
1 | def p' : Point := Point.mk 1 2 -- 通过构造器构造 |
如果我们希望改用其他名称,可以在一开始定义结构体 Point 时,加上一行
1 | structure Point where |
此时可以通过 Point.mymaker 1 2 来定义 Point 类型数据。
这部分知识和 Python 的面向对象编程有点类似,p.xxx 是以 p 作为 self 参数去执行调用方法。
本节回顾:
- 结构体通过
structure 结构体名 where (x1 : 类型1) ... deriving Repr的方式定义,使用{}进行初始化。 - 在拷贝数据时,可用
with方法,比如{p with x:=1}。 - 用
.方法访问结构体内容,p.func本质上执行了Point.func,并以p作为匹配到的最左侧的参数。
数据类型,模式和递归
这节开始,考察抽象的理解能力。
数据类型
前边介绍了结构体,多个独立的数据块组合成一个连贯的整体,作为全新的类型。这种将一组值组合在一起的类型(如结构体)称为积类型(Product Type)。然而,许多领域的概念不能自然地表示为结构体,例如计算器的二元运算符,加法、减法和乘法。结构体无法提供一种简单的方法来编码多项选择。
结构体是跟踪固定字段集的绝佳方式,但许多应用程序需要可能包含任意数量元素的数据。大多数经典的数据结构(例如树和列表)具有递归结构,其列表的尾部本身是一个列表,或者二叉树的左右分支本身是二叉树。在计算器中,加法表达式中的加数本身可能是乘法表达式。
允许选择的类型称为和类型(Sum Type),而可以包含自身实例的类型称为递归类型(Recursive Datatype)。递归和类型称为归纳类型(Inductive Datatype),因为可以用数学归纳法来证明有关它们的陈述。在编程时,归纳类型通过模式匹配和递归函数来转化。
许多内置类型是标准库中的归纳类型。例如,Bool 就是一个归纳类型:
1 | inductive Bool where |
第一行定义新类型(Bool)的名称,而其余各行分别描述了一个构造子。
与结构体的构造子一样,归纳类型的构造子用于产生该类型的元素。与结构体不同,归纳类型可以有多个构造子。这里有两个构造子,true 和 false,并且都不接受任何参数。这些构造子保存在类型同名的命名空间,例如 Bool.true 和 Bool.false。在 Lean 标准库中,true 和 false 从此命名空间中重新导出,以便可以单独编写它们。
举个例子:
1 | inductive Demo where |
和抽象类型不同,比如
1 | abstract type Bool end |
在面向对象的示例中,True 和 False 都是比 Bool 更具体的类型,而 Lean 定义仅引入了新类型 Bool。
归纳数据类型 Nat 的定义如下:
1 | inductive Nat where |
在这里,构造子 zero 表示 0 属于 Nat,而构造子 succ 表示 (n : Nat) 的后继也属于 Nat。通过这两个构造子,我们能表达整个自然数集。
同样地,为了表达 Nat,在其他语言中需要定义三个类型:
1 | abstract type Nat end |
这样会定义比 Lean 中等价的项更多的类型。此外,这个示例突出显示了 Lean 构造子更像是抽象类的子类,而不是像 C# 或 Java 中的构造函数。
注:Lean 构造子对应于 JavaScript 或 TypeScript 中的对象,这些对象包含一个标识内容的标记。
模式匹配
在很多语言中,这类数据首先会使用 instance-of 运算符来检查接收了哪个子类,然后读取给定子类中可用的字段值。instance-of 会检查确定要运行哪个代码,以确保此代码所需的数据可用,而数据由字段本身提供。在 Lean 中,这两个目的均由模式匹配(Pattern Matching)实现。
使用模式匹配的函数示例是 isZero,这是一个当其参数为 Nat.zero 时返回 true 的函数,否则返回 false。
1 | def isZero (n : Nat) : Bool := |
match 表达式为函数参数 n 提供了解构。若 n 由 Nat.zero 构建,则采用模式匹配的第一分支,结果为 true。若 n 由 Nat.succ 构建,则采用第二分支,结果为 false。
isZero Nat.zero 的逐步求值过程如下:
1 | isZero Nat.zero |
isZero 5 的求值过程类似:
1 | isZero 5 |
isZero 中模式的第二分支中的 k 并非装饰性符号。它使 succ 的参数 Nat 可见,并提供了名称。然后可以使用该较小的数字计算表达式的最终结果。
正如某个数字 n的后继比 n 大 1(即 n+1),某个数字的前驱比它小 1。如果 pred 是一个查找 Nat 前驱的函数,那么以下示例应该能得到预期的结果:
1 | #eval pred 5 |
由于 Nat 无法表示负数,因此 0 有点令人费解。在使用 Nat 时,会产生负数的运算符通常会被重新定义为产生 0 本身:
1 | #eval pred 0 |
要查找 Nat 的前驱,第一步是检查它是使用哪个构造子创建的。如果是 Nat.zero,则结果为 Nat.zero。如果是 Nat.succ,则使用名称 k 引用其下的 Nat。而这个 Nat 即是所需的前驱,因此 Nat.succ 分支的结果是 k。
1 | def pred (n : Nat) : Nat := |
将此函数应用于 5 会产生以下步骤:
1 | pred 5 |
模式匹配不仅可以用于和类型,还可用于结构体。例如,一个从 Point3D 中提取第三维度的函数可以写成如下:
1 | def depth (p : Point3D) : Float := |
在这种情况下,直接使用 z 访问器会简单得多,但结构体模式有时是编写函数的最简单方法。
递归函数
引用正在定义的名称的定义称为递归定义(Recursive Definition)。归纳数据类型允许是递归的,事实上,Nat 就是这样的数据类型的一个例子,因为 succ 需要另一个 Nat。递归数据类型可以表示任意大的数据,仅受可用内存等技术因素限制。就像不可能在数据类型定义中为每个自然数编写一个构造器一样,也不可能为每个可能性编写一个模式匹配用例。
递归数据类型与递归函数可以很好地互补。一个简单的 Nat 递归函数是检查其参数是否是偶数。在这种情况下,zero 是偶数。像这样的代码的非递归分支称为 基本情况(Base Case)。奇数的后继是偶数,偶数的后继是奇数。这意味着使用 succ 构建的数字当且仅当其参数不是偶数时才是偶数。
1 | def even (n : Nat) : Bool := |
这种思维模式对于在 Nat 上编写递归函数是非常典型的。首先,确定对 zero 做什么。然后,确定如何将任意 Nat 的结果转换为其后继的结果,并将此转换应用于递归调用的结果。此模式称为 结构化递归(Structural Recursion)。
不同于许多语言,Lean 默认确保每个递归函数最终都会到达基本情况。从编程角度来看,这排除了意外的无限循环。但此特性在证明定理时尤为重要,而无限循环会产生重大的困难。由此产生的一个结果是,Lean 不会接受尝试对原始数字递归调用自身的 even 版本:
1 | def evenLoops (n : Nat) : Bool := |
错误消息的主要部分是 Lean 无法确定递归函数是否最终会到达基本情况(因为它不会)。
1 | fail to show termination for |
尽管加法需要两个参数,但只需要检查其中一个参数。要将零加到数字 n 上,只需返回 n。要将 k 的后继加到 n 上,则需要得到将 k 加到 n 的结果的后继。
1 | def plus (n : Nat) (k : Nat) : Nat := |
在 plus 的定义中,选择名称 k' 表示它与参数 k 相关联,但并不相同。例如,展开 plus 3 2 的求值过程会产生以下步骤:
1 | plus 3 2 |
考虑加法的一种方法是 n+k 将 Nat.succ 应用于 n k 次。类似地,乘法 n×k 将 n 加到自身 k 次,而减法 n−k 将 n 的前驱求得 k 次。
1 | def times (n : Nat) (k : Nat) : Nat := |
1 | def minus (n : Nat) (k : Nat) : Nat := |
并非每个函数都可以轻松地使用结构化递归来编写。将加法理解为迭代的 Nat.succ,将乘法理解为迭代的加法,将减法理解为迭代的前驱,这表明除法可以实现为迭代的减法。在这种情况下,如果分子小于分母,则结果为零。否则,结果是将分子减去分母除以再除以分母所得的后继。
1 | def div (n : Nat) (k : Nat) : Nat := |
只要第二个参数不为 0,这个程序就会终止,因为它始终朝着基本情况前进。然而,它不是结构化递归,因为它不遵循「为零找到一个结果,然后将较小的 Nat 的结果转换为其后继的结果」的模式。特别是,该函数的递归调用,应用于另一个函数调用的结果,而非输入构造子的参数。因此,Lean 会拒绝它,并显示以下消息:
1 | fail to show termination for |
此消息表示 div 需要手动证明停机。这个主题在最后一章中进行了探讨。
多态
基础概念
和大多数语言一样,Lean 中的类型可以带有参数。例如,类型 List Nat 描述的是自然数列表,List String 描述的是字符串列表,而 List (List Point) 描述的是点的列表的列表。这与 C# 或 Java 等语言中的 List<Nat>,List<String> 或 List<List<Point>> 非常相似。就像 Lean 使用空格来将参数传递给函数一样,它也使用空格来将参数传递给类型。
在函数式编程中,术语“多态性”通常指带有类型参数的数据类型和定义。这与面向对象编程社区的做法不同,在面向对象编程中,术语通常指的是可能覆盖其超类某些行为的子类。在本书中,“多态性”总是指这个词的第一个意义。这些类型参数可以在数据类型或定义中使用,这使得可以使用任何通过将参数的名称替换为其他类型来得到的类型对数据类型或定义进行操作。
Point 结构要求 x 和 y 字段都是 Float 类型。然而,点并没有要求每个坐标都具有特定的表示方式。一种多态版本的 Point 称为 PPoint,它可以将类型作为参数,并使用该类型来表示两个字段:
1 | structure PPoint (α : Type) where |
就像函数定义的参数紧跟在被定义的名称之后一样,结构体的参数紧跟在结构体名称之后。当没有更具体的名称可用时,Lean 常用希腊字母来命名类型参数。Type 是用来描述其他类型的类型,因此 Nat、List String 和 PPoint Int 都具有类型 Type。
就像 List 一样,可以通过提供特定的类型作为其参数来使用 PPoint:
1 | def natOrigin : PPoint Nat := |
在这个例子中,两个字段都预期是 Nat 类型的。就像一个函数通过用实际参数值替换其形式参数来被调用一样,把类型 Nat 作为参数提供给 PPoint,会得到一个结构体,其中字段 x 和 y 的类型是 Nat,因为参数名 α 已被参数类型 Nat 替换了。在 Lean 中,类型是普通的表达式,因此给多态类型(像 PPoint)传递参数不需要任何特殊的语法。
定义也可以接受类型作为参数,从而使它们具有多态性。函数 replaceX 用一个新值替换 PPoint 的 x 字段。为了让 replaceX 能够适用于任何多态的点,它必须具有多态性。这通过使其第一个参数成为点字段的类型来实现,后面的参数引用第一个参数的名字来实现。
1 | def replaceX (α : Type) (point : PPoint α) (newX : α) : PPoint α := |
简言之,当参数 point 和 newX 的类型中涉及到 α 时,它们是指向 作为第一个参数提供的任何类型。这与函数参数名在函数体中引用提供的值的方式类似。
可以通过让 Lean 检查 replaceX 的类型,然后再检查 replaceX Nat 的类型来看到这一点。
1 | #check (replaceX) |
1 | replaceX : (α : Type) → PPoint α → α → PPoint α |
这种函数类型包括第一个参数的 name,后面的参数在类型中引用这个 name。就像函数应用的值是通过在函数体中用提供的参数值替换参数名来找到的一样,函数应用的类型是通过在函数的返回类型中用提供的值替换参数名来找到的。提供第一个参数 Nat 导致类型中剩余部分的所有 α 的出现都被替换为 Nat:
1 | #check replaceX Nat natOrigin |
1 | replaceX Nat natOrigin : Nat → PPoint Nat |
因为剩余的参数没有显式命名,所以当提供更多的参数时,不会发生进一步的替换:
1 | #check replaceX Nat natOrigin |
1 | replaceX Nat natOrigin : Nat → PPoint Nat |
1 | #check replaceX Nat natOrigin 5 |
1 | replaceX Nat natOrigin 5 : PPoint Nat |
整个函数应用表达式的类型是通过将类型作为参数传递来确定的这一事实并不影响其能否进行求值。
1 | #eval replaceX Nat natOrigin 5 |
1 | { x := 5, y := 0 } |
多态函数通过接受一个命名的类型参数并让后续类型引用参数的名称来工作。然而,类型参数并没有什么可以让它们被命名的特殊之处。
给定一个表示正负号的数据类型:
1 | inductive Sign where |
可以编写一个函数,其参数是一个符号。如果参数为正数,函数将返回一个 Nat,而如果参数为负数,则返回一个 Int:
1 | def posOrNegThree (s : Sign) : |
由于类型是一等公民,可以使用 Lean 语言的普通规则进行计算,它们可以通过对数据类型进行模式匹配来进行计算。当 Lean 检查这个函数时,它使用函数体中的 match-表达式与类型中的 match-表达式相匹配,使得 Nat 成为 pos 情况的预期类型,使得 Int 成为 neg 情况的预期类型。
将 posOrNegThree 应用于 Sign.pos,结果就是函数体和返回类型中的参数名 s 被 Sign.pos 替代。求值可以同时发生在表达式和它的类型中:
1 | (posOrNegThree Sign.pos : match Sign.pos with | Sign.pos => Nat | Sign.neg => Int) |
链表
Lean 的标准库包含了一个经典的链表数据类型,称为 List,并且有特殊的语法来方便使用。链表可以用方括号表示。例如,一个包含小于 10 的质数的链表可以写成:
1 | def primesUnder10 : List Nat := [2, 3, 5, 7] |
在幕后,List 是一个归纳数据类型,它的定义如下:
1 | inductive List (α : Type) where |
这个定义表明 List 对于给定类型 α 是一个多态(Type*)的类型。它有两个构造器:
nil: List α表示空列表。cons: α -> List α -> List α表示非空列表,包含一个头部元素α和一个尾部子列表List α。
和标准库中的实际定义稍有不同,因为它使用了尚未介绍的功能,但其基本相似。
该定义表明 List 接受一个类型作为其参数,就像 PPoint 一样。这个类型是列表中存储的条目的类型。根据构造函数,List α 可以使用 nil 或 cons 来构建。构造函数 nil 表示空列表,构造函数 cons 用于非空列表。cons 的第一个参数是列表的头,第二个参数是其尾部。一个包含 n 个条目的列表包含 n 个 cons 构造函数,其中最后一个以 nil 作为其尾部。
标准库定义:
1 | inductive List (α : Type u) where |
通过直接 List 的构造函数,primesUnder10 的示例可以更明确地写为:
1 | def explicitPrimesUnder10 : List Nat := |
这两个定义是完全等价的,但是 primesUnder10 比 explicitPrimesUnder10 更易读。
使用 List 的函数可以与使用 Nat 的函数以相同的方式定义。事实上,一种考虑链表的方式是将其视为一个 Nat,每个 succ 构造函数都悬挂着一个额外的数据字段。从这个角度来看,计算列表的长度的过程是将每个 cons 替换为 succ,将最终的 nil 替换为 zero。就像 replaceX 将点的字段类型作为参数一样,length 接受列表项的类型。例如,如果列表包含字符串,则第一个参数是 String:length String ["Sourdough", "bread"]。它会这样计算:
1 | length String ["Sourdough", "bread"] |
length 的定义既是多态的(因为它将列表项类型作为参数),又是递归的(因为它引用了自身)。通常,函数遵循数据的形状:递归数据类型对应递归函数,多态数据类型对应多态函数。
1 | def length (α : Type) (xs : List α) : Nat := |
传统上,xs 和 ys 这样的名称被惯例性地用来代表未知值的列表。名称中的 s 表示它们是复数形式,因此读作 “exes” 和 “whys”,而不是 “x s” 和 “y s”。
为了更容易阅读列表上的函数,可以使用括号符号 [] 来模式匹配 nil,而中缀符号 :: 可以替代 cons:
1 | def length (α : Type) (xs : List α) : Nat := |
注:这里的记号定义和 haskell 有点像。
隐式参数
replaceX 和 length 在使用时有一些繁文缛节,因为类型参数通常可以由后续的值唯一确定。事实上,在大多数语言中,编译器完全能够自动确定类型参数,只有偶尔需要用户的帮助。在 Lean 中也是如此。当定义一个函数时,可以通过用花括号而不是括号括起来来声明参数为 隐式参数 。例如,一个带有隐式类型参数的replaceX版本如下:
1 | def replaceX {α : Type} (point : PPoint α) (newX : α) : PPoint α := |
因为 Lean 可以从后续参数中推断出 α 的值,所以可以在不显式提供 Nat 的情况下,使用 natOrigin 函数。
1 | #eval replaceX natOrigin 5 |
1 | { x := 5, y := 0 } |
类似地,length 可以被重新定义,使输入类型隐式地被接收:
1 | def length {α : Type} (xs : List α) : Nat := |
这个 length 函数可以直接应用于 primesUnder10:
1 | #eval length primesUnder10 |
标准库中,Lean 将这个函数称为 List.length,这意味着用于结构体字段访问的点语法也可以用于获取列表的长度:
1 | #eval primesUnder10.length |
就像 C# 和 Java 需要时通常需要显式提供类型参数一样,Lean 并不总能自动找到隐式参数。在这些情况下,可以通过提供参数名来指定它们。例如,只适用于整数列表的 List.length 的版本可以通过将 α 设置为 Int 来指定:
1 | #check List.length (α := Int) |
1 | List.length : List Int → Nat |
更多的内置数据类型
除了列表之外,Lean 的标准库还包含许多其他结构体和归纳数据类型,可用于各种场景。
Option 可选类型
并非每个列表都有第一个条目,有些列表是空的。许多集合操作可能无法得出它们正在查找的内容。例如,查找列表中第一个条目的函数可能找不到任何此类条目。因此,必须有一种方法来表示没有第一个条目。
许多编程语言都有一个表示缺少值的 null 值。Lean 提供了一个叫做 Option 的数据类型,它为某个其他类型提供了一个指示缺失值的标志。例如,可为空的 Int 被表示为 Option Int,而可为空的字符串列表被表示为类型 Option (List String)。引入一个新的类型来表示可为空性意味着类型系统确保不能忘记对 null 进行检查,因为 Option Int 不能在需要 Int 的上下文中使用。
Option 有两个构造函数,分别称为 some 和 none,分别表示基础类型的非空和空版本。非空构造函数 some 包含基础值,而 none 不带参数:
1 | inductive Option (α : Type) : Type where |
Option 类型与 C# 和 Kotlin 等语言中的可空类型非常相似,但并非完全相同。在这些语言中,如果一个类型(比如 Boolean)总是引用该类型的实际值(true 和 false),那么类型 Boolean? 或 Nullable<Boolean> 则额外允许 null 值。在类型系统中跟踪这一点非常有用:类型检查器和其他工具可以帮助程序员记住检查 null,并且通过类型签名明确描述可空性的 API 比不描述可空性的 API 更具有信息性量。
然而,这些可空类型与 Lean 的 Option 在一个非常重要的方面有所不同,那就是它们不允许多层可选项性。Option (Option Int) 可以用 none、some none 或 some (some 360) 构造。另一方面,C# 禁止多层可空性,只允许将 ? 添加到不可空类型,而 Kotlin 将 T?? 视为等同于 T?。这种细微的差别在实践中大多无关紧要,但有时会很重要。
要查找列表中的第一个条目(如果存在),请使用 List.head?。问号是名称的一部分,与在 C# 或 Kotlin 中使用问号表示可空类型并不相同。在 List.head? 的定义中,下划线用于表示列表的尾部。在模式匹配中,下划线匹配任何内容,但不会引入变量来引用匹配的数据。使用下划线而不是名称是一种向读者清楚传达输入部分被忽略的方式。
1 | def List.head? {α : Type} (xs : List α) : Option α := |
Lean 的命名约定是使用后缀 ? 定义可能失败的操作,用于返回 Option 的版本,! 用于提供无效输入时崩溃的版本,D 用于在操作在其他情况下失败时返回默认值的版本。例如,head 要求调用者提供数学证据证明列表不为空,head? 返回 Option,head! 在传递空列表时使程序崩溃,headD 采用一个默认值,以便在列表为空时返回。问号和感叹号是名称的一部分,而不是特殊语法,因为 Lean 的命名规则比许多语言更自由。
由于 head? 在 List 命名空间中定义,因此它可以使用访问器记法:
1 | #eval primesUnder10.head? |
然而,尝试在空列表上进行测试会导致两个错误:
1 | #eval [].head? |
1 | don't know how to synthesize implicit argument |
这是因为 Lean 无法完全确定表达式的类型。特别是,它既无法找到 List.head? 的隐式类型参数,也无法找到 List.nil 的隐式类型参数。在 Lean 的输出中,?m.XYZ 表示无法推断出来的程序的一部分。这些未知部分被称为“元变量”,它们出现在一些错误消息中。为了评估一个表达式,Lean 需要能够找到其类型,而该类型不可用是因为空列表没有任何条目可供找到其类型。显式提供类型使 Lean 能够继续进行:
1 | #eval [].head? (α := Int) |
该类型也可以用类型注释提供:
1 | #eval ([] : List Int).head? |
错误信息提供了有用的线索。两条消息都使用同一个元变量来描述缺失的隐式参数,这意味着 Lean 已经确定了这两个缺失的部分将共享一个解决方案,尽管它无法确定解决方案的实际值。
Prod 积类型
Prod 结构,即 “Product”,是一种将两个值结合在一起的通用方法。例如,一个 Prod Nat String 包含一个 Nat 和一个 String。换句话说,PPoint Nat 可以被替换为 Prod Nat Nat。Prod 很像 C# 中的元组 (tuples),Kotlin 中的 Pair 和 Triple 类型,以及 C++ 中的 tuple。许多应用最好通过定义自己的结构来实现,即使是像 Point 这样简单的情况,因为使用领域术语可以使代码更加易读。此外,定义结构体类型有助于通过为不同的领域概念分配不同的类型来捕获更多错误,防止它们混淆。
另一方面,在某些情况下,定义新类型的开销可能不值得。此外,一些库非常通用,没有比 “pair” 更具体的概念。最后,标准库包含了各种便利函数,可以更轻松地处理内置的 pair 类型。
标准的 pair 结构称为 Prod。
1 | structure Prod (α : Type) (β : Type) : Type where |
列表的使用如此频繁,以至于有特殊的语法使它们更具可读性。
出于同样的原因,积类型及其构造子都有特殊的语法。类型 Prod α β 通常写为 α × β,反映了集合的笛卡尔积的常用记法。与此类似,偶对的常用数学记法可用于 Prod。换句话说,不必写:
1 | def fives : String × Int := { fst := "five", snd := 5 } |
我们只需要写下下面这个定理:
1 | def fives : String × Int := ("five", 5) |
两种表示法都是右结合的。这意味着以下定义是等价的:
1 | def sevens : String × Int × Nat := ("VII", 7, 4 + 3) |
换句话说,所有超过两种类型的积及其对应的构造子,实际上都是嵌套的积和嵌套的偶对。
Sum 和类型
和(Sum) 数据类型是一种允许在两种不同类型的值之间进行选择的一般方式。例如,Sum String Int 要么是 String,要么是 Int。与 Prod 一样,Sum 应该在编写非常通用的代码时使用,对于没有合适的特定领域类型的一小段代码,或者当标准库包含有用的函数时使用。在大多数情况下,使用自定义归纳类型更具可读性和可维护性。
Sum α β 类型的取值要么是应用于 α 类型的构造子 inl,要么是应用于 β 类型的构造子 inr:
1 | inductive Sum (α : Type) (β : Type) : Type where |
这些名称分别是「左注入(left injection)」和「右注入(right injection)」的缩写。就像笛卡尔积符号用于 Prod 一样,「圆圈加号」符号用于 Sum,因此 α ⊕ β 是 Sum α β 的另一种记法。Sum.inl 和 Sum.inr 没有特殊语法。
例如,如果宠物名称可以是狗名或猫名,那么它们的类型可以作为字符串的和来引入:
1 | def PetName : Type := String ⊕ String |
在实际的程序中,通常最好为这个目的定义一个自定义的归纳数据类型,以便具有信息性的构造函数名称。比如:
1 | inductive PetName2 (α : Type) (β : Type) where |
在这里,Sum.inl 用于狗的名字,Sum.inr 用于猫的名字。可以使用这些构造函数来编写一个动物名字的列表:
1 | def animals : List PetName := |
模式匹配可用于区分两个构造子。例如,一个函数用于统计动物名称列表中狗的数量(即 Sum.inl 构造子的数量),如下所示:
1 | def howManyDogs (pets : List PetName) : Nat := |
函数调用在中缀运算符之前进行求值,因此 howManyDogs morePets + 1 等同于 (howManyDogs morePets) + 1。如预期所见,#eval howManyDogs animals 返回的结果是 3。
注:留意 Sum 和 Prod 的区别,前者为 inductive 定义的归纳类型,后者为 structure 定义的结构体。
Unit
Unit 是仅有一个无参构造子的类型,称为 unit。换句话说,它只描述了一个单一的值,该值由该构造函数应用于没有任何参数的结果组成。Unit 的定义如下:
1 | inductive Unit : Type where |
单独使用时,Unit 并不是特别有用。但是,在多态代码中,它可以用作缺少数据的占位符。例如,以下归纳数据类型表示算术表达式:
1 | -- ann : Type 是一个类型参数,表示"标注"(annotation) |
类型参数 ann 表示标注,每个构造子都有标注。来自解析器的表达式可能带有源码位置标注,因此 ArithExpr SourcePos 的返回类型需要确保解析器在每个子表达式中放置 SourcePos。然而,不来自于解析器的表达式没有源码位置,因此它们的类型可以是 ArithExpr Unit。
创建一个简单的表达式:3 + 4
1 | -- 类型:ArithExpr Unit 表示"不需要标注信息的算术表达式" |
当然,我们也可以直接定义不带标注的算术类型:
1 | inductive ArithExpr2 : Type where |
此外,由于所有 Lean 函数都有参数,因此其他语言中的零参数函数可以表示为接受 Unit 参数的函数。在返回位置,Unit 类型类似于 C 的语言中的 void。在 C 系语言中,返回 void 的函数会将控制权返回给调用者,但不会返回任何有意义的值。Unit 作为一个特意表示无意义的值,可以在类型系统无需具有特殊用途的 void 特性的情况下表达这一点。Unit 的构造子可以写成空括号:() : Unit。
Empty 空类型
Empty 数据类型没有任何构造函数。因此,它表示不可达代码,因为没有一系列的调用能以类型 Empty 的值终止。
1 | inductive Empty : Type |
Empty 并不像 Unit 那样经常使用。然而,在一些特定的上下文中它是有用的。许多多态数据类型在它们的所有构造函数中并不都使用它们的所有类型参数。例如,Sum.inl 和 Sum.inr 只使用了 Sum 的一个类型参数。使用 Empty 作为 Sum 的类型参数之一可以在程序的特定位置上排除一个构造函数。这可以允许在具有额外限制的上下文中使用通用代码。
命名:求和、积和单位
一般来说,提供多个构造子的类型称为和类型(Sum Type),而其单个构造子接受多个参数的类型称为积类型(Product Type)。这些术语与普通算术中使用的和与积有关。当涉及的类型包含有限数量的值时,这种关系最容易看出。如果 α 和 β 是分别包含 n 和 k 个不同值的数据类型,则 α ⊕ β 包含 n+k 个不同值,α × β 包含 n×k 个不同值。
例如,Bool 有两个值:true 和 false,Unit 有一个值:Unit.unit。积 Bool × Unit 有两个值 (true, Unit.unit) 和 (false, Unit.unit),和 Bool ⊕ Unit 有三个值 Sum.inl true、Sum.inl false 和 Sum.inr unit。类似地,2×1=2,2+1=3。
可能会遇到的错误
并非所有可定义的结构或归纳类型都可以具有类型 Type。特别地,如果一个构造函数接受任意类型作为参数,则归纳类型必须具有不同的类型。这些错误通常与 “universe levels” 有关。例如,对于这个归纳类型:
1 | inductive MyType : Type where |
Lean 会给出以下错误:
1 | invalid universe level in constructor 'MyType.ctor', parameter 'α' has type |
稍后的章节会描述为什么会出现这种情况,以及如何修改定义使其正常运作。在现在,试着将类型作为整个归纳类型的参数,而不是构造函数的参数。
类似地,如果构造函数的参数是一个以正在定义的数据类型为参数的函数,那么该定义会被拒绝。例如:
1 | inductive MyType : Type where |
产生了以下的消息:
1 | (kernel) arg #1 of 'MyType.ctor' has a non positive occurrence of the datatypes being declared |
由于技术原因,允许这些数据类型可能会破坏 Lean 的内部逻辑,使其不适合作为定理证明器使用。
忘记归纳类型的参数也可能产生令人困惑的消息。例如,当 ctor 的类型中没有传递参数 α 到 MyType 的时候:
1 | inductive MyType (α : Type) : Type where |
Lean 回复了以下错误:
1 | type expected, got |
错误消息显示 MyType 的类型是 Type → Type,它本身并不描述类型。MyType 需要一个参数来成为一个真正的类型。
在其他情况下,例如在定义的类型签名中省略了类型参数,可能会出现相同的消息:
1 | inductive MyType (α : Type) : Type where |
练习题
- 编写一个函数,找到列表中的最后一个元素。它应该返回一个
Option。 - 编写一个函数,找到列表中满足给定条件的第一个元素。函数的定义开始部分为
def List.findFirst? {α : Type} (xs : List α) (predicate : α → Bool) : Option α := - 编写一个函数
Prod.swap,交换一对中的两个字段。函数的定义开始部分为def Prod.swap {α β : Type} (pair : α × β) : β × α := - 重新编写
PetName示例,使用自定义的数据类型,并将其与使用Sum的版本进行比较。 - 编写一个函数
zip,将两个列表合并成一个元素为对的列表。结果列表的长度应该与输入列表的最短长度相同。函数的定义开始部分为def zip {α β : Type} (xs : List α) (ys : List β) : List (α × β) :=。 - 编写一个多态函数
take,返回列表中的前n个条目,其中n是一个Nat。 如果列表包含的条目少于n个,则结果列表应为输入列表。#eval take 3 ["bolete", "oyster"]应当产生["bolete", "oyster"],而#eval take 1 ["bolete", "oyster"]应当产生["bolete"]。 - 使用类型和算术的类比,编写一个将乘积分配给和的函数。换句话说,它的类型应为
α × (β ⊕ γ) → (α × β) ⊕ (α × γ)。 - 使用类型和算术的类比,编写一个将乘以二转变成和的函数。换句话说,它的类型应为
Bool × α → α ⊕ α。
其他便利功能
Lean 包含了许多便利功能,这使得程序更加简洁。
自动隐式参数
在 Lean 中编写多态函数时,通常不需要列出所有的隐式参数。相反,它们可以简单地被提到。如果 Lean 可以确定它们的类型,那么它们会自动作为隐式参数插入。换句话说,之前的 length 定义可以简化为:
1 | def length {α : Type} (xs : List α) : Nat := |
可以不使用 {α : Type} 来写出 LEAN 定理证明的文章。
1 | def length (xs : List α) : Nat := |
这可以大大简化那些需要许多隐式参数的高度多态定义。
模式匹配定义
在使用 def 定义函数时,常常会给参数命名,然后立即使用模式匹配来处理这个参数。例如,在 length 中,参数 xs 只在 match 中使用。在这种情况下,可以直接编写match 表达式的不同情况,而不需要给参数命名。
第一步是将参数的类型移到冒号的右边,这样返回类型就是一个函数类型。例如,length 的类型是 List α → Nat。然后,用模式匹配的每个情况替换 :=:
1 | def length : List α → Nat |
这种语法也可以用来定义接受多个参数的函数。在这种情况下,它们的模式之间用逗号分隔。例如,drop 函数接受一个数字 \( n \) 和一个列表,并返回删除了前 \( n \) 个元素后的列表。
1 | def drop : Nat → List α → List α |
已命名的参数和模式也可以在同一定义中使用。例如,一个函数接受一个默认值和一个可选值,当可选值为 none 时返回默认值,可以写成:
1 | def fromOption (default : α) : Option α → α |
这个函数在标准库中被称为 Option.getD,可以使用点表示法调用:
1 | #eval (some "salmonberry").getD "" |
1 | #eval none.getD "" |
局部定义
在计算过程中,给中间步骤命名常常是有用的。在很多情况下,中间值本身就代表了有用的概念,显式地命名可以使程序更易读。在其他情况下,中间值被使用了多次。与大多数其他语言一样,在 Lean 中将代码写两次会导致计算两次,而将结果保存在变量中则会保存和重复使用计算结果。
例如,unzip 是一个将一对列表转换为一对列表的函数。当一对列表为空时,unzip 的结果是一对空列表。当一对列表的头部有一对值时,该值的两个字段将被添加到解压剩余列表的结果中。unzip 的定义正是按照上述描述来的:
1 | def unzip : List (α × β) → List α × List β |
不幸的是,存在一个问题:这段代码的运行速度比需求要慢。列表中的每一个元素都会导致两次递归调用,这使得该函数花费指数级的时间。然而,两次递归调用的结果是相同的,所以没有必要进行两次递归调用。
在 Lean 中,可以使用 let 命名并保存递归调用的结果。使用 let 进行局部定义与使用 def 进行顶层定义类似:它需要一个待在局部定义中的名称、可选的参数、类型签名,然后是跟在 := 后面的实现体。在局部定义之后,该局部定义所在的表达式(称为 let-表达式的 主体)必须在一个新行上,并且要在文件中的列号小于或等于 let 关键字的列号。例如,let 可以在 unzip 中这样使用:
1 | def unzip : List (α × β) → List α × List β |
在单行上使用 let 时,需要用分号将局部定义与主体分隔开来。
在使用 let 进行局部定义时,当一个模式足以匹配某个数据类型的所有情况时,可以使用模式匹配。在 unzip 函数中,递归调用的结果是一个二元组。因为二元组只有一个构造函数,所以可以用一个二元组模式来替换 unzipped 的名称:
1 | def unzip : List (α × β) → List α × List β |
使用 let 带有模式的明智用法可以使代码更易读,相比手动编写访问器调用。
let 和 def 之间最大的区别是递归 let 定义必须通过显式写入 let rec 来表示。例如,反转列表的一种方法涉及到一个递归的辅助函数,就像下面的定义一样:
1 | def reverse (xs : List α) : List α := |
等价写法:
1 | def rhelper : List α → List α → List α |
类型推断
在许多情况下,Lean 可以自动确定表达式的类型。在这些情况下,无需在顶级定义(使用 def)和局部定义(使用 let)中显式提供类型注解。例如,对 unzip 的递归调用不需要注解:
1 | def unzip : List (α × β) → List α × List β |
作为一个经验法则,通常可以省略文字值(如字符串和数字)的类型,尽管 Lean 可能会选择比意图更具体的字面数字类型。在函数应用中,Lean通常可以确定类型,因为它已经知道了参数类型和返回类型。省略函数定义的返回类型通常是可以的,但函数参数通常需要注释。在示例中的 unzipped 这样的非函数定义,如果它们的主体不需要类型注释,就不需要类型注释,而这个定义的主体是一个函数应用。
在使用显式的 match 表达式时,可以省略 unzip 的返回类型:
1 | def unzip (pairs : List (α × β)) := |
一般来说,宁可多加类型标注,也不要太少。首先,显式类型向读者传达了对代码的假设。即使 Lean 可以自行确定类型,但无需反复查询 Lean 以获取类型信息,代码仍然更容易阅读。其次,显式类型有助于定位错误。程序对其类型越明确,错误消息就越有信息量。这在 Lean 这样的具有非常丰富的类型系统的语言中尤为重要。第三,显式类型使编写程序变得更容易。类型是一种规范,编译器的反馈可以成为编写符合规范的程序的有用工具。最后,Lean 的类型推断是一种尽力而为的系统。由于 Lean 的类型系统非常丰富,因此无法为所有表达式找到「最佳」或最通用的类型。这意味着即使你得到了一个类型,也不能保证它是给定应用的「正确」类型。例如,14 可以是 Nat 或 Int:
1 | #check 14 |
缺少类型注解会导致混乱的错误信息。在 unzip 的定义中省略所有类型注解:
1 | def unzip pairs := |
导致了有关 match 表达式的信息:
1 | invalid match-expression, pattern contains metavariables |
这是因为 match 需要知道被检查值的类型,但该类型不可用。“元变量”是程序中的一个未知部分,错误消息中用 ?m.XYZ 来表示——它们在多态一节中进行了描述。在这个程序中,参数的类型注解是必需的。
即使是一些非常简单的程序也需要类型注解。例如,恒等函数只是返回传入的参数。加上参数和类型注解,它看起来像这样:
1 | def id (x : α) : α := x |
Lean 能够自行确定返回类型:
1 | def id (x : α) := x |
然而,省略参数类型会导致错误:
1 | def id x := x |
1 | failed to infer binder type |
通常,像“无法推断”这样的消息或者提及到元变量的消息往往是需要更多类型注释的标志。特别是在学习 Lean 的过程中,最好将大部分类型提供明确的注释。
同时匹配
与定义时的模式匹配类似,模式匹配表达式也可以同时匹配多个值。要检查的表达式和要匹配的模式都用逗号隔开,与定义中的语法类似。下面是使用同时匹配的 drop 的一个版本:
1 | def drop (n : Nat) (xs : List α) : List α := |
自然数的模式
在 数据类型模式和递归 部分,even 定义如下:
1 | def even (n : Nat) : Bool := |
就像列表模式的特殊语法比直接使用 List.cons 和 List.nil 更具可读性一样,自然数可以使用字面数字和 + 进行匹配。例如,even 也可以这样定义:
1 | def even : Nat → Bool |
在此记法中,+ 模式的参数扮演着不同的角色。在幕后,左参数(上面的 n)成为一些 Nat.succ 模式的参数,右参数(上面的 1)确定包裹该模式的 Nat.succ 数量有多少。
halve 中的显式模式将 Nat 除以二并丢弃余数:
1 | def halve : Nat → Nat |
可以写为:
1 | def halve : Nat → Nat |
在幕后,这两个定义完全等价。记住:halve n + 1 等价于 (halve n) + 1,而非 halve (n + 1)。
在使用这个语法时,+ 的第二个参数应始终是一个字面量 Nat。尽管加法是可交换的,但是在模式中交换参数可能会产生以下错误:
1 | def halve : Nat → Nat |
匿名函数
在 Lean 中,函数不一定要在顶层进行定义。作为表达式,函数可以使用 fun 语法来生成。函数表达式以关键字 fun 开始,接着是一个或多个参数,这些参数与返回表达式使用 => 进行分隔。例如,可以编写一个将数字加 1 的函数:
1 | #check fun x => x + 1 |
1 | fun x => x + 1 : Nat → Nat |
类型注释的书写方式与 def 函数定义一样,使用括号和冒号:
1 | #check fun (x : Int) => x + 1 |
1 | fun x => x + 1 : Int → Int |
同样,隐式参数可以用花括号来书写:
1 | #check fun {α : Type} (x : α) => x |
1 | fun {α} x => x : {α : Type} → α → α |
这种形式的匿名函数表达式通常被称为 lambda 表达式,因为在数学描述编程语言时,使用希腊字母 λ(lambda),而 Lean 使用 fun 关键字。尽管 Lean 允许使用 λ 替代 fun,但通常还是写作 fun。需要注意的是,fun 不能显示指定函数返回类型,而只能靠类型推断。
匿名函数也支持在 def 中使用的多模式风格。例如,一个如果存在自然数的前驱则返回它的函数可以写作:
1 | #check fun |
1 | fun x => |
注意,输出的 Lean 函数的描述本身有一个命名参数和一个 match 表达式。许多 Lean 的便利的语法缩写在后台被展开为更简单的语法,但有时会泄漏抽象。
使用 def 定义带有参数的函数可以重写为函数表达式。例如,一个将其参数加倍的函数可以写成以下形式:
1 | def double : Nat → Nat := fun |
当匿名函数非常简单时,例如 fun x => x + 1,创建函数的语法会相当冗长。在此例中,有六个非空白字符用于引入函数,其函数体仅包含三个非空白字符。对于这些简单的情况,Lean 提供了一个简写。在括号包围的表达式中,间点号 · 可以表示一个参数,括号内的表达式为函数体,因此该函数也可以写成 (· + 1)。
间点号总是将最靠近的一对括号创建为函数。例如,(· + 5, 3) 是返回一对数字的函数,而 ((· + 5), 3) 是一个函数和一个数字的偶对。
1 | #check (· + 5, 3) |
如果使用多个点,则它们按从左到右的顺序成为参数:
1 | (· , ·) 1 2 |
其作用等效于
1 | fun x y => (x, y) |
匿名函数可以与使用 def 或 let 定义的函数完全相同的方式进行应用。命令 #eval (fun x => x + x) 5 的结果为 10,与 #eval (· * 2) 5 的结果相同。
由于匿名函数不声明类型,虽然下边函数在 def 中会报错:
1 | def iditenty x := x |
但在 fun 可以正常编译:
1 | fun x => x |
命名空间
Lean 中的每个名称都存在于一个命名空间中,命名空间是一组名称的集合。使用 . 将名称放置在命名空间中,因此 List.map 是 List 命名空间中的名称 map。即使它们在其他方面是相同的,不同命名空间中的名称也不会发生冲突。这意味着 List.map 和 Array.map 是不同的名称。命名空间可以嵌套,因此 Project.Frontend.User.loginTime 是嵌套命名空间 Project.Frontend.User 中的名称 loginTime。
可以在命名空间中直接定义名称。例如,名称 double 可以在 Nat 命名空间中定义:
1 | def Nat.double (x : Nat) : Nat := x + x |
因为 Nat 也是一个类型的名称,所以对于类型为 Nat 的表达式,可以使用点符号来调用 Nat.double:
1 | #eval (4 : Nat).double |
除了直接在命名空间中定义名称外,也可以使用 namespace 和 end 命令将一系列声明放在命名空间中。例如,下面的代码将在命名空间 NewNamespace 中定义 triple 和 quadruple:
1 | namespace NewNamespace |
在这个例子中,triple 和 quadruple 分别是在命名空间 NewNamespace 中定义的两个函数。在命名空间内部,它们可以使用命名空间作为限定符进行访问,例如 NewNamespace.triple 和 NewNamespace.quadruple。这样做可以避免命名冲突,特别是当在不同的命名空间中定义相同名称的函数时。
为了引用它们,使用 NewNamespace. 作为它们名称的前缀:
1 | #check NewNamespace.quadruple |
命名空间可以被“打开”,这样可以在不必显式限定的情况下使用其中的名称。在表达式之前写上 open MyNamespace in 可以使 MyNamespace 的内容在表达式中可用。例如,在打开 NewNamespace 之后,timesTwelve 使用了 quadruple 和 triple。
1 | def timesTwelve (x : Nat) := |
命名空间也可以在命令之前打开。这样可以使命令的所有部分都可以引用命名空间的内容,而不仅仅是单个表达式。为了做到这一点,在命令之前加上 open ... in 语句。
1 | open NewNamespace in |
open 不只适用于 Namespace,对函数等任意名称都适用,比如:
1 | def iditenty : Int -> Int := (fun x => x) |
或者,把某个数据类型里定义的函数打开:open Nat Real。不过,如果在全局打开,可能会导致命名空间冲突:
1 | open identity |
最后一行报错:
1 | ambiguous, possible interpretations |
还有一个行为,在 namespace 内部定义变量时,如果变量在外部已存在,也不会出现调用冲突,而是始终使用内部的变量,此时 open 打开的同名变量会被屏蔽,除非显式引用。
if let
在使用具有和类型的值时,通常只对一个构造子感兴趣。例如,给定一个表示 Markdown 内联元素子集的类型:
1 | inductive Inline : Type where |
我们可以编写一个识别字符串元素并提取它们内容的函数:
1 | def Inline.string? (inline : Inline) : Option String := |
这个函数的主体可以使用 if 和 let 的方式来替代编写:
1 | def Inline.string? (inline : Inline) : Option String := |
这与模式匹配 let 的语法非常相似,不同之处在于它可以与和类型一起使用,因为在 else 的情况中提供了备选项。在某些情况下,使用 if let 代替 match 可以让代码更易读。
位置结构参数
结构体部分 提供了两种构建结构的方法:
- 可以直接调用构造函数,例如
Point.mk 1 2。 - 可以使用花括号标记,例如
{ x := 1, y := 2 }。
在某些情况下,通过位置而不是通过名称传递参数可能更方便,但又不直接命名构造函数。例如,定义各种相似的结构类型可以帮助保持领域概念的分离,但是自然阅读代码的方式可能会将它们视为元组。在这些情况下,参数可以用尖括号 ⟨ 和 ⟩ 包围起来。一个 Point 可以写作 {{#example_in Examples/Intro.lean pointPos}}。请注意!尽管它们看起来像小于号 < 和大于号 >,但这些括号是不同的。可以分别使用 \< 和 \> 输入它们。
就像使用命名构造函数参数的花括号标记一样,此位置语法仅在 Lean 可以从类型注解或程序中的其他类型信息中确定结构的类型的上下文中使用。例如,#eval ⟨1, 2⟩ 会产生以下错误:
1 | invalid constructor ⟨...⟩, expected type must be an inductive type |
错误中的元变量是因为没有可用的类型信息。添加注释会解决这个问题,比如在 #eval (⟨1, 2⟩ : Point) 中。
1 | { x := 1.000000, y := 2.000000 } |
字符串插值
在 Lean 中,使用 s! 作为字符串的前缀会触发 插值,其中大括号中包含的表达式会被替换为它们的值。这与 Python 的 f 字符串和 C# 的 $ 前缀字符串类似。例如,
1 | #eval s!"three fives is {NewNamespace.triple 5}" |
得到输出
1 | "three fives is 15" |
并非所有的表达式都可以插入字符串中进行内插。例如,尝试插入一个函数会导致错误。
1 | #check s!"three fives is {NewNamespace.triple}" |
产出是一个 Markdown 格式的文章。请提供输入,我将翻译成中文。
1 | failed to synthesize instance |
这是因为没有标准的方法将函数转换为字符串。Lean 编译器维护了一个表,描述了如何将不同类型的值转换为字符串,而 failed to synthesize instance 这个消息意味着Lean 编译器在该表中没有找到给定类型的条目。这使用了结构体部分一节中描述的 deriving Repr 语言特性。
总结
表达式的求值
在 Lean 中,当表达式被求值时会发生计算。这遵循数学表达式的常规规则:子表达式按照常规的运算顺序被替换为它们的值,直到整个表达式变为一个值。在计算 if 或 match 语句时,分支中的表达式在找到条件或匹配对象的值之前不会被求值。
一旦它们被赋予一个值,变量就不会再改变。与数学类似但与大多数编程语言不同,Lean 的变量只是值的占位符,而不是可以写入新值的地址。变量的值可以来自使用 def 进行的全局定义,使用 let 进行的局部定义,作为函数的命名参数,或来自模式匹配。
函数
在 Lean 中,函数是一等公民,意味着它们可以作为参数传递给其他函数,保存在变量中,并像任何其他值一样使用。每个 Lean 函数接受且只接受一个参数。为了编码接受多个参数的函数,Lean 使用一种称为柯里化(currying)的技术,其中提供第一个参数返回一个期望接收剩余参数的函数。为了编码不接受参数的函数,Lean 使用了 Unit 类型,它是可能的最不具信息的参数。
有三种主要的创建函数的方式:
- 使用
fun编写匿名函数。
例如,可以将交换Point的字段的函数写为fun (point : Point) => { x := point.y, y := point.x : Point }。 - 通过圆括号中的一个或多个居中的点
·来编写非常简单的匿名函数。每个居中的点都成为函数的一个参数,而括号限定了它的主体。例如,将从其参数中减去 one 的函数可以写为(· - 1)而不是fun x => x - 1。 - 使用
def或let进行函数定义,可以通过添加参数列表或使用模式匹配的语法。
类型
Lean 检查每个表达式是否具有类型。比如 Int、Point、{α : Type} → Nat → α → List α 和 Option (String ⊕ (Nat × String)),描述了可能最终找到的表达式的值。与其他语言一样,Lean 中的类型可以表达程序的轻量级规范,并由 Lean 编译器进行检查,从而省去了某些类型的单元测试的需要。与大多数语言不同的是,Lean 的类型可以表示任意的数学概念,将编程和定理证明的世界统一起来。虽然在这本书中,我们主要不会使用 Lean 来证明定理,但是《Theorem Proving in Lean 4》这本书中包含了更多关于这一主题的信息。
有些表达式可以有多个类型。例如,3 可以是一个 Int 或者一个 Nat。在 Lean 中,应该将其理解为两个不同的表达式,一个类型是 Nat,另一个类型是 Int,它们恰巧使用了相同的写法,而不是将它们看作是同一个东西的不同类型。
Lean 有时可以自动推断类型,但是用户通常需要提供类型信息。这是因为 Lean 的类型系统非常灵活。
即使 Lean 能够找到一个类型,它可能不是我们想要的类型 —— 如果没有进一步的约束条件,3 可能被认为是一个 Nat,而不是一个 Int。一般来说,最好是明确地写出大部分类型,只有非常明显的类型可以让 Lean 自动推导。这有助于改进 Lean 的错误信息,并使程序员的意图更加清晰。
有些函数或数据类型接受类型作为参数,它们被称为 多态。多态使得编写像计算列表长度这样的程序时,不需要关心列表中的元素的具体类型。由于 Lean 中的类型是一等公民,多态不需要任何特殊的语法,因此类型可以像其他参数一样传递。在函数类型中给参数命名可以使后面的类型引用到该参数,并且将该函数应用到一个参数上的类型可以通过用参数的值替换参数的名称来确定。
结构体和归纳类型
Lean 可以使用 structure 或 inductive 特性引入全新的数据类型。即使其定义完全相同,这些新类型也不被认为与任何其他类型等价。数据类型有 构造函数 来解释如何构造其值,并且每个构造函数都接受一定数量的参数。在 Lean 中,构造函数与面向对象语言中的构造函数不同:Lean 的构造函数是惰性的数据持有者,而不是初始化已分配对象的活动代码。
通常情况下,structure 用于引入一个积类型(即只有一个构造函数且可以接受任意数量参数的类型),而 inductive 用于引入一个和类型(即有多个不同的构造函数的类型)。使用 structure 定义的数据类型会为构造函数的每个参数提供一个访问函数。结构体和归纳数据类型都可以使用模式匹配来使用,模式匹配使用调用所述构造子的语法的一个子集来表达存储在构造子中的值。模式匹配知道如何创建值就意味着知道如何使用它。
递归
在定义中,当所定义的名称在其定义自身中使用时,该定义就是递归的。由于 Lean 既是交互式定理证明器又是编程语言,对递归定义有一些限制。在 Lean 的逻辑方面,循环定义可能会导致逻辑不一致。
为了确保递归定义不破坏 Lean 的逻辑方面,Lean 必须能够证明所有递归函数在调用任何参数时都终止。实际上,这意味着递归调用都在输入的结构较小的部分上进行,这确保了始终向基本情况的进展,或者用户必须提供一些其他证据来证明函数始终终止。同样,递归归纳类型不允许具有将函数作为参数接收的构造函数,因为这将使得编码非终止函数成为可能。